diff --git a/00011_Trigonometry_Crossing_the_river/en_article_proofreading.md b/00011_Trigonometry_Crossing_the_river/en_article_proofreading.md
index 6a2bbb7..0ef3c77 100644
--- a/00011_Trigonometry_Crossing_the_river/en_article_proofreading.md
+++ b/00011_Trigonometry_Crossing_the_river/en_article_proofreading.md
@@ -8,42 +8,45 @@ is_finished: False
# Crossing the river
-The ferryman must get from his dock on the river bank to the other
-which is on the opposite bank $500\ \text{m}$ downstream. At
-this part of the river, the river has no bends, flows at a speed of $2\ \text{m}/\text{s}$ and is
-$100\ \text{m}$ wide. We also know that the ferryman's ship is moving at a speed relative to the water
-$12\ \text{km}/\text{h}$.
+The ferryman must get from his dock on one river bank to the other dock,
+which is located on the opposite bank, $500\ \text{m}$ downstream. The river between the docks is straight and
+$100\ \text{m}$ wide. The speed of the current is $2\ \text{m}/\text{s}$.
+We also know that the ferryman's boat moves at a speed of
+$12\ \text{km}/\text{h}$ relative to the water.
-> **Exercise 1.** By how many degrees should the ferryman turn his ship from the direct course to the destination?
+> **Exercise 1.**
+The ferryman wants to travel directly from one dock to the other. He can achieve this by angling the boat across the river and maintaining this direction. By what angle should the ferryman turn his boat from the direct path to travel straight to the other dock?
+<!-- Česká verze:
+Převozník se chce dostat přímou cestou z jednoho přístaviště do druhého. Toho dosáhne, pokud loď natočí více napříč přes řeku a tento směr lodi bude držet. O jaký úhel má převozník natočit svou loď od přímého směru, aby plul přímou cestou k druhému přístavišti? -->
-*Solution.* Let's denote the starting dock $A$ and the destination dock $B$ and then
-denote $P$ the foot of the perpendicular line from point $B$ to the opposite bank of the river. Further
-let's mark out the vectors of river velocity, ship speed relative to the water and total velocity
-of the ship on the water at the starting point $A$:
+*Solution.* Let us denote by $A$ and $B$ the starting and destination point. Also, denote
+by $P$ the foot of the perpendicular line from point $B$ to the opposite bank of the river.
+Next, mark the vectors of the current's velocity, the boat’s velocity relative to the water, and the resulting velocity
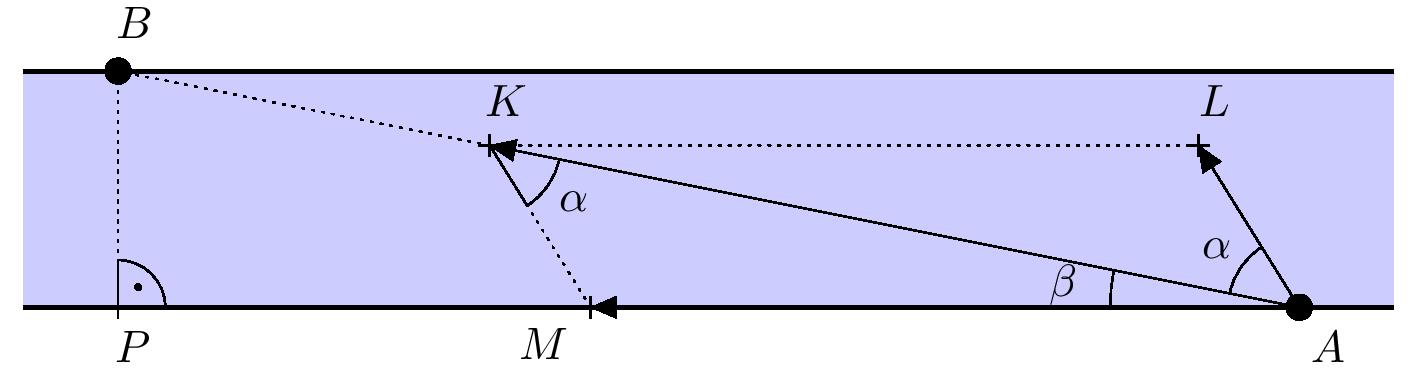
+of the boat (boat’s velocity relative to the river's bottom) all with their initial points at point A and endpoints as follows (see the figure):
-- $\overrightarrow{AM}$ is the velocity vector of the river current;
-- $\overrightarrow{AL}$ is the velocity vector of the ship relative to the water (not including
- current);
-- $\overrightarrow{AK}$ is the vector of the resultant velocity relative to the Earth's surface
- (current + water speed).
+- $\overrightarrow{AM}$ is the vector of the current's velocity.
+- $\overrightarrow{AL}$ is the vector of the boat’s velocity relative to the water (not including
+ current).
+- $\overrightarrow{AK}$ is the vector of the resulting velocity of the boat relative to the river's bottom
+ (current + boat velocity).
-Given that $K\in AB$ and according to the vector addition rule, the quadrilateral
-$MALK$ is a parallelogram. Our task is to determine the magnitude of the angle $KAL$, which we denote by
-$\alpha$.
+ <!--V tomto odstavečku ja kauzalita špatně, tak jsem se to pokusila přeformulovat, aby to lépe dávalo smysl.-->
+Since $K\in AB$, our task is to determine the angle $KAL$, which we denote by
+$\alpha$. By the vector addition rule, the quadrilateral $MALK$ is a parallelogram.
-
-Let's denote $\lvert \sphericalangle MAK \rvert = \beta$, therefore $\lvert
-\sphericalangle MAL \rvert = \alpha + \beta$. From the assignment we know, that $|BP|=100\
-\text{m}$ a $|AP|=500\ \text{m}$; by using the tangent function in the right-angled
-triangle $PAB$ we get $\beta = \arctg\,\frac{1}{5}$.
+
-Since a parallelogram is bisected by its diagonal into two congruent triangles, it holds
+Further, let's denote $\lvert \sphericalangle MAK \rvert = \beta$. Then $\lvert \sphericalangle MAL \rvert = \alpha + \beta$. It is given that $|BP|=100\
+\text{m}$ and $|AP|=500\ \text{m}$. By using the tangent function in the right-angled
+triangle $PAB$ we get $\beta = \arctan\frac{1}{5} \approx 11^{\circ}19'$.
+<!-- Pro přibližné hodnoty se místo rovnítka s tečkou v angličtině používá dvojtá vlnovka. -->
+
+Since a parallelogram is bisected by its diagonal into two congruent triangles, it holds that
$\lvert \sphericalangle AKM \rvert= \lvert \sphericalangle KAL \rvert = \alpha$.
-To calculate $\alpha$ we use law of sines for the triangle $AKM$, since the sizes
-$|KM|$ and $|AM|$ of its sides correspond to the actual magnitudes of the given velocities.
-After converting to a common unit (km/h in our solution), we get specifically
-$|KM|=12$ and $|AM|=2\cdot 3{,}6=7{,}2$. We now express from the law of sines:
+To calculate $\alpha$, we use the law of sines for the triangle $AKM$.
+After converting the side lengths to a common unit (km in our solution), we get specifically
+$|KM|=12\ \text{km}$ and $|AM|=2\cdot 3.6=7.2\ \text{km}$. We now express $\alpha$ from the law of sines:
$$
\begin{aligned}
@@ -51,42 +54,53 @@ $$
\sin \alpha &= \frac{|AM|}{|KM|}\cdot \sin\beta \qquad \Rightarrow \qquad \alpha = \arcsin \left( \frac{|AM|}{|KM|}\cdot \sin\beta \right)
\end{aligned}
$$
-After substituting specific values, we get $\beta \doteq 11^{\circ}19'$ and $\alpha
-\doteq 6^{\circ}45'$. The ferryman thus has to turn his ship by approximately $7^{\circ}$
-to the right as opposed to the straight course to the destination.
+After substituting the values, we obtain $\alpha
+\approx 6^{\circ}45'$. Thus, the ferryman has to turn his boat by approximately $7^{\circ}$
+to the right from the direct course to the destination.
+
+>**Exercise 2.** If the digital clock on the boat shows 11:00 at the moment of departure
+>(without showing seconds), what time will the clock show at the moment the boat arrives at the other
+>dock?
+<!-- V prezentovaném řešení se nejprve provedení odhadu neuvádí, ani komentář k tomu, jak by se měl odhad provést. Navrhuji větičku (Estimate the result first.) ze zadání raději vynechat. -->
+
+
+
->**Exercise 2.** If the digital clock on the ship shows 11:00 at the moment of departure
->(seconds don't show), what time will the clock show at the moment the ship arrives to the other
->dock? Estimate the result first.
-*Solution.* Let's first determine the distance between the two docks using the Pythagorean theorem
-of the right triangle $ABP$:
+
+*Solution.* Let's first determine the distance between the two docks using the Pythagorean theorem in the right-angled triangle $ABP$:
$$
\begin{aligned}
|AB| &= \sqrt{|AP|^2 + |BP|^2}\\
-|AB| &= \sqrt{0{,}5^2 + 0{,}1^2}\ \text{km}\\
-|AB| &\doteq 0{,}51\ \text{km}.
+|AB| &= \sqrt{0.5^2 + 0.1^2}\\
+|AB| &\approx 0.51\ \text{km}.
\end{aligned}
$$
+<!-- V anglické verzi příkladu by desetinná čárka měla být nahrazena tečkou -->
+Now, we determine the magnitude of the resultant velocity of the boat relative to the river’s bottom, which is
+equal to the length of the line segment $AK$. This, for example, can be determined using the law of cosines in
+triangle $AKM$. We denote the interior angle $\lvert \sphericalangle AMK \rvert =\gamma$, which measures $180^{\circ}-\alpha - \beta \approx 161^{\circ}56'$. Then for $|AK|$ we can write:
+<!-- Myslím, že úhel gama by také měl být vyznačen v obrázku. -->
-Now we need to determine the magnitude of the speed of the ship relative to the earth's surface, which is
-equal to the size of the segment $AK$. This can be determined, for example, from the law of cosines for
-triangle $AKM$. The interior angle $\gamma$ adjacent to the vertex $M$ has the size
-$180^{\circ}-\alpha - \beta$.
$$
\begin{aligned}
|AK| &= \sqrt{|KM|^2 + |AM|^2 - 2\cdot |KM| \cdot |AM| \cdot \cos \gamma}\\
|AK| &= \sqrt{12^2 + 2^2 - 2\cdot 12 \cdot 2 \cdot \cos(161^{\circ}56')}\\
-|AK| &\doteq 19{,}0
+|AK| &\approx 19.0\ \text{km}
\end{aligned}
$$
-The ship travels a path of $0{,}51\ \text{km}$ at a speed of $19\ \text{km}/\text{h}$, which takes
+The boat travels a direct path of $0.51\ \text{km}$ at an average speed of $19\ \text{km}/\text{h}$, which takes:
$$
\begin{aligned}
-t &= \frac{s}{v}\\
-t &= \frac{0{,}51}{19}\ \text{h}\\
+t &= \frac{distance\ traveled}{average\ speed}\\
+t &= \frac{0.51}{19}\ \text{h}\\
\end{aligned}
$$
-i.e. approximately 97 seconds. At the finish line, the clock will show 11:01 or 11:02.
+<!-- značení s/t neodpovídá anglické terminologii, lépe je to zapsat slovy, než zavádět nestandardní nové značení -->
+
+which is approximately 97 seconds. Therefore, the clock will show 11:01 or 11:02 upon arrival at the target dock.
+
+
+