diff --git a/00010_Analytic_geometry_Parabolic_calculator/en_article_proofreading.md b/00010_Analytic_geometry_Parabolic_calculator/en_article_proofreading.md
index a253498..af7ac2d 100644
--- a/00010_Analytic_geometry_Parabolic_calculator/en_article_proofreading.md
+++ b/00010_Analytic_geometry_Parabolic_calculator/en_article_proofreading.md
@@ -2,20 +2,21 @@
keywords:
- analytic geometry
- parametric equation of line
-is_finished: Nearly
+is_finished: False
---
# Parabolic calculator
+<!--Tereza: Můj komentář ke změnám navrženým v tomto souboru najete na konci. -->
-While surfing the Internet, Eva found one interesting thing about the graph of a function
-$f\colon y = x^2$ which can be used as a calculator to multiply two numbers
+While surfing the Internet, Eva found an interesting fact about the graph of a function
+$f\colon y = x^2$ which is that the graph can be used as a calculator to multiply two numbers
$a$ and $b$.[^1] The procedure is as follows:
- 1. On the axis $x$ mark the images of the numbers $-a$ and $b$.
- 2. Draw the perpendicular lines to the $x$-axis at these points and
- construct its intersections with the graph of the function $f$.
- 3. A line passing through the intersections just constructed
- intersects the axis $y$ at the point, whose distance from the
+ 1. On the $x$-axis mark the points corresponding to the numbers $-a$ and $b$.
+ 2. At these points, draw lines perpendicular to the $x$-axis and
+ construct their intersections with the graph of the function $f$.
+ 3. The line passing through the newly constructed intersections
+ intersects the $y$-axis at a point whose distance from the
origin is $ab$.
You can try the procedure in the attached worksheet, its illustrations
@@ -25,28 +26,26 @@ is also available in GeoGebra. The interactive applet can be found on the websit
> **Exercise 1.** Does the above procedure apply to all pairs of
> numbers, or only to some? Can this procedure be proved?
-*Solution.* The procedure shows that if the images of $-a$ and $b$
-merge, the line described in the third point cannot be constructed
-uniquely. Given procedure will therefore not work if $-a=b$ holds. We
-will show that besides this case the procedure holds for all other
+*Solution.* It is evident from the procedure that if the images of the numbers $-a$ and $b$
+merge, the line described in the third step cannot be uniquely constructed.
+Therefore, the given procedure will not work if $-a=b$ holds. We
+will show that, besides this case, the procedure holds for all other
pairs of numbers $a$ and $b$.
-Let's construct the image of $-a$ and $-b$ on the $x$ axis according
-to the procedure in the problem and then construct perpendicular lines
-to the $x$-axis at these points. Let's denote the intersections of
-these perpendiculars with the parabola $A$ and $B$, and denote the
-line $AB$ by $p$. The line $p$ intersects the axis $y$ at the point
-$C$, which determines the unknown number $m$.
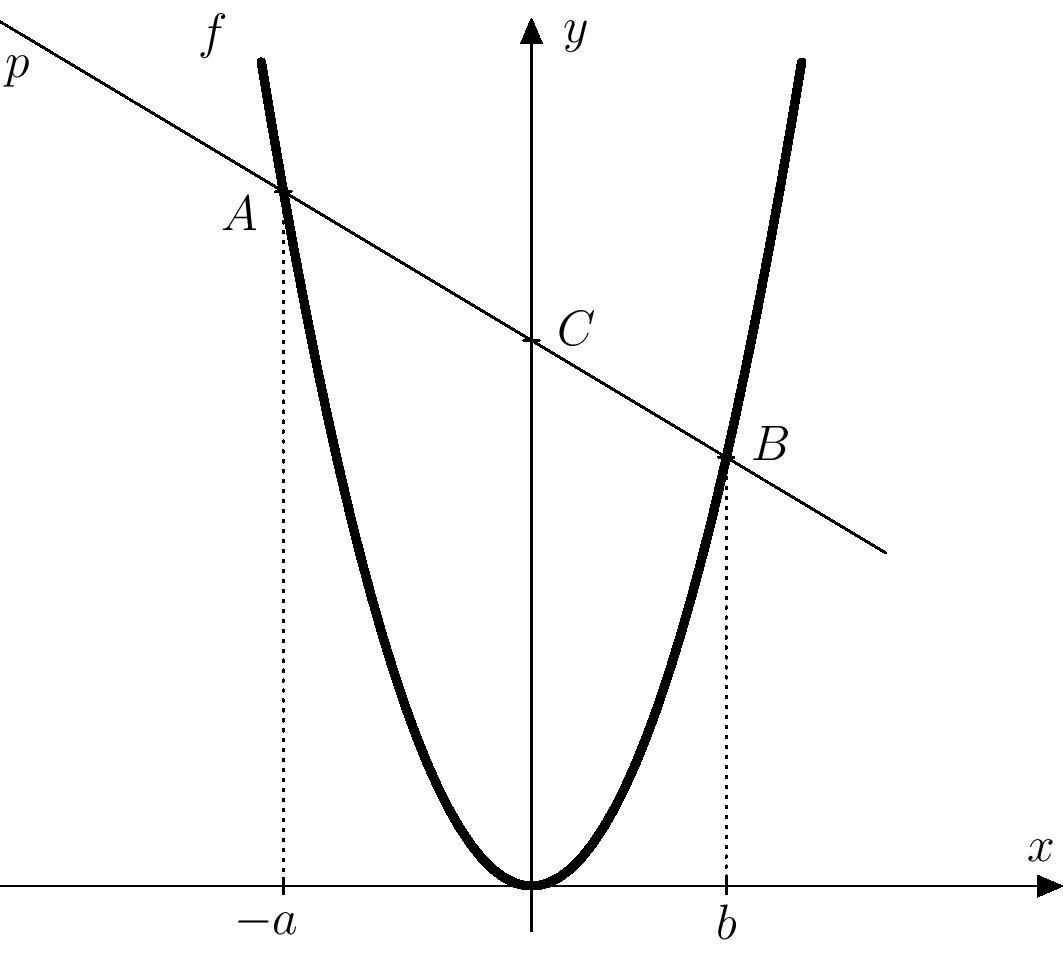
+Let's construct, according to the given procedure, on the $x$-axis the points corresponding to the numbers $-a$ and $-b$, and then construct perpendiculars at these points
+to the $x$-axis. Let's denote the intersections of
+these perpendiculars with the parabola by $A$ and $B$, and let the
+line $AB$ be denoted by $p$. The line $p$ intersects the $y$ axis at the point $C$, which determines the unknown number $m$.
-The line $p$ is given by two points $A[-a;a^2]$ and $B[b;b^2]$, so the
+The line $p$ is defined by the points $A(-a;a^2)$ and $B(b;b^2)$, so the
direction vector is
-$$\overrightarrow{u}=\overrightarrow{AB}= (b+a; b^2-a^2).$$
+$$\overrightarrow{u}=\overrightarrow{AB}= [b+a; b^2-a^2].$$
By multiplying the vector $\overrightarrow{u}$ with the number
$\frac{1}{a+b}$ we get
-$$\overrightarrow{u}=(1; b-a).$$
-This adjustment can be made since for our case $b\neq a$ is
+$$\overrightarrow{u}=[1; b-a].$$
+This adjustment can be made since in our case is $b\neq a$, and so
$b+a\neq0$. Thus, we get the parametric equations
$$
\begin{aligned}
@@ -56,23 +55,34 @@ y &= b^2 + t\cdot (b-a), t\in\mathbb{R}
\end{aligned}
$$
-By substituting the coordinates of the point $C$ into the left sides
-of the equations (i.e. $x=0$, $y=m$) we get system of equations
+By substituting the coordinates of point $C$ into the left sides
+of the equations (i.e. $x=0$, $y=m$) we get the system
$$
\begin{aligned}
0 &= b+t\\
m &= b^2+t(b-a)
\end{aligned}
$$
-We express $t=-b$ from the first equation and substitute it into the
+From the first equation, we express $t=-b$ and substitute it into the
second equation. From here
$$
\begin{aligned}
m &=b^2+(-b)\cdot(b-a) \\
-m &=ab,
+m &=ab.
\end{aligned}
$$
-which we had to prove.
+This is the result we needed to prove.
[^1]: In general, graphs that allow us to perform arithmetic operations
by geometric constructions are called *nomograms*.
+
+<!-- Tereza: V souboru jsem provedla opět více úprav. Upravovala jsem členy, čárky, slovosled, ale i významově některé formulace neodpovídají. Zdůvodňovat v tomto množství všechny změny je náročné, proto prosím, kdyby jste s mými změnami nesouhlasili, ráda to s vámi proberu a pokusím se své návrhy na změny zdůvodnit.
+
+Některé provedené změny ale přeci okomentuji:
+Např nesouhlasím s formulací "konstrukce obrazů čísel na ose x". za lepší považuji (i v češtině) formulaci "konstrukce bodů odpovídajících číslům a a b, protože "obrazy" těchto bodů jsou vlastně na grafu kvadratické funkce, tedy jsou to ty průsečíky. Prostě stadrdně v matematice na ose x jsou body a na funkci jsou jejich obrazy " Tomu odpovídá pár mnou navržených změn v tomto příkladu.
+
+Dále jsem např. změnila značení bodů a vektorů - tj druh použitých závorek. V anglických mat. textech se (bohužel ale je to tak) používají závorky standardně naopak. Tj kulaté pro souřadnice bodů a hranaté pro vektory. Takto je značení použito i v ostatních anglických příkladech v Math4U.
+Bod A(a,b)
+Vektor u=[a,b]
+
+ -->
\ No newline at end of file