diff --git a/00008_Solid_Geometry-Distance_of_cities/en_article_proofreading.md b/00008_Solid_Geometry-Distance_of_cities/en_article_proofreading.md
index 3890cfa..304a83d 100644
--- a/00008_Solid_Geometry-Distance_of_cities/en_article_proofreading.md
+++ b/00008_Solid_Geometry-Distance_of_cities/en_article_proofreading.md
@@ -1,12 +1,12 @@
---
keywords:
- - stereometry
- - planimetry
+ - solid geometry
+ - plane geometry
- circle
- geography
-is_finished: False
+is_finished: True
---
-# Distances on the Earth's surface
+# Distances on the Earth's Surface
Which of the routes between Lisbon and Washington shown on the map is shorter?
@@ -22,13 +22,13 @@ so it actually corresponds to an arc on a circle that closely resembles a parall
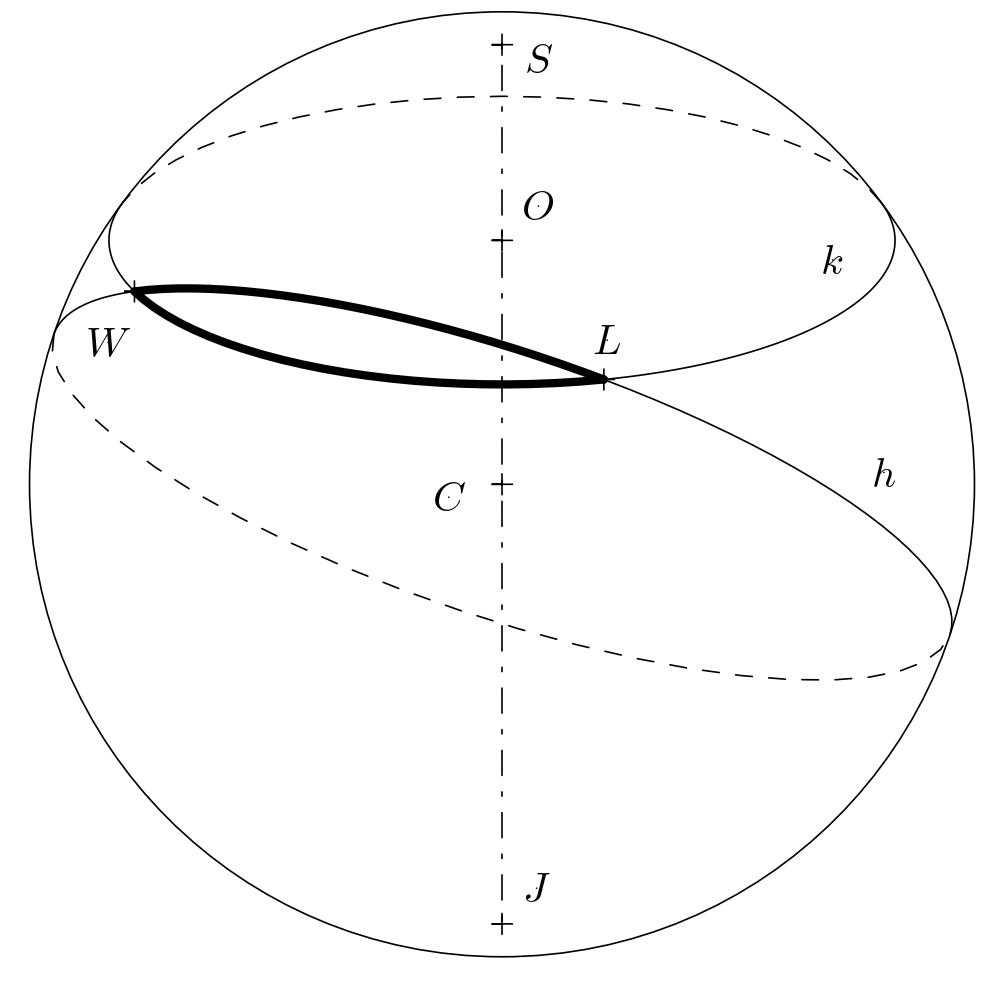
However, on the spherical surface (which we will consider to be the Earth's surface in this task),
-the shortest distance is another arc. This arc lies on a circle $h$ whose center $C$ is the center of the Earth.
+the shortest distance is another arc. This arc is a part of a circle $h$ whose center $C$ is the center of the Earth.
We refer to such paths as *orthodromes* and call all circles with this property *great circles*.
-However, how many kilometers do we save by traveling along an orthodrome?
+How many kilometers do we save by traveling along an orthodrome?
The answer to this question has to be calculated.
### Dictionary
-* *Latitude* of a point on the Earth's surface (expressed in degrees and north/south orientation) is the angle between a straight line that passes through the given point and the center of the Earth and the plane of the equator.
+* *Latitude* of a point on the Earth's surface (expressed in degrees and north/south orientation) is the angle between a straight line that passes through the given point and the center of the Earth and the equatorial plane.
* *Longitude* of a point on the Earth's surface (expressed in degrees and east/west orientation) is the angle between the plane of the meridian that passes through the given point and the plane of the zero meridian.
> **Exercise.** Lisbon and Washington are located
@@ -38,44 +38,47 @@ The answer to this question has to be calculated.
> Lisbon is located at approximately $9^{\circ}$ west longitude.
> Washington is located at $77^{\circ}$ west longitude.
> Let us assume that the Earth is a sphere with center $C$ and radius
-> $6\ 371\,\text{km}$ and that the plane flies at an average altitude of
+> $6,371\,\text{km}$ and that the plane flies at an average altitude of
> $10\,\text{km}$ (take-off and landing are not taken into account).
> Therefore, in all considerations, we will work with a sphere of radius
-> $\varrho=6\ 381\,\text{km}$.
+> $\varrho=6,381\,\text{km}$.
*Solution.* First, let's determine how many kilometers the plane
-will travel while traveling along the parallel.
+will cover while traveling along the parallel.
Let us denote the parallel at $39^{\circ}$ north latitude as a circle $k$ with center $O$ and radius $r$.
-In a suitable rectangular projection of the globe (see the figure, where $S$ and $J$ are the poles),
-this circle appears as a segment $AB$ with center $O$.
-
-In an appropriate rectangular projection of the globe (see the figure,
-where $S$ and $J$ are the poles), this circle appears as a segment $AB$
-with center $O$.
+In an appropriate orthogonal projection of the globe (see the figure, where $S$ and $J$ are the poles),
+this circle appears as a chord $AB$ with center $O$.
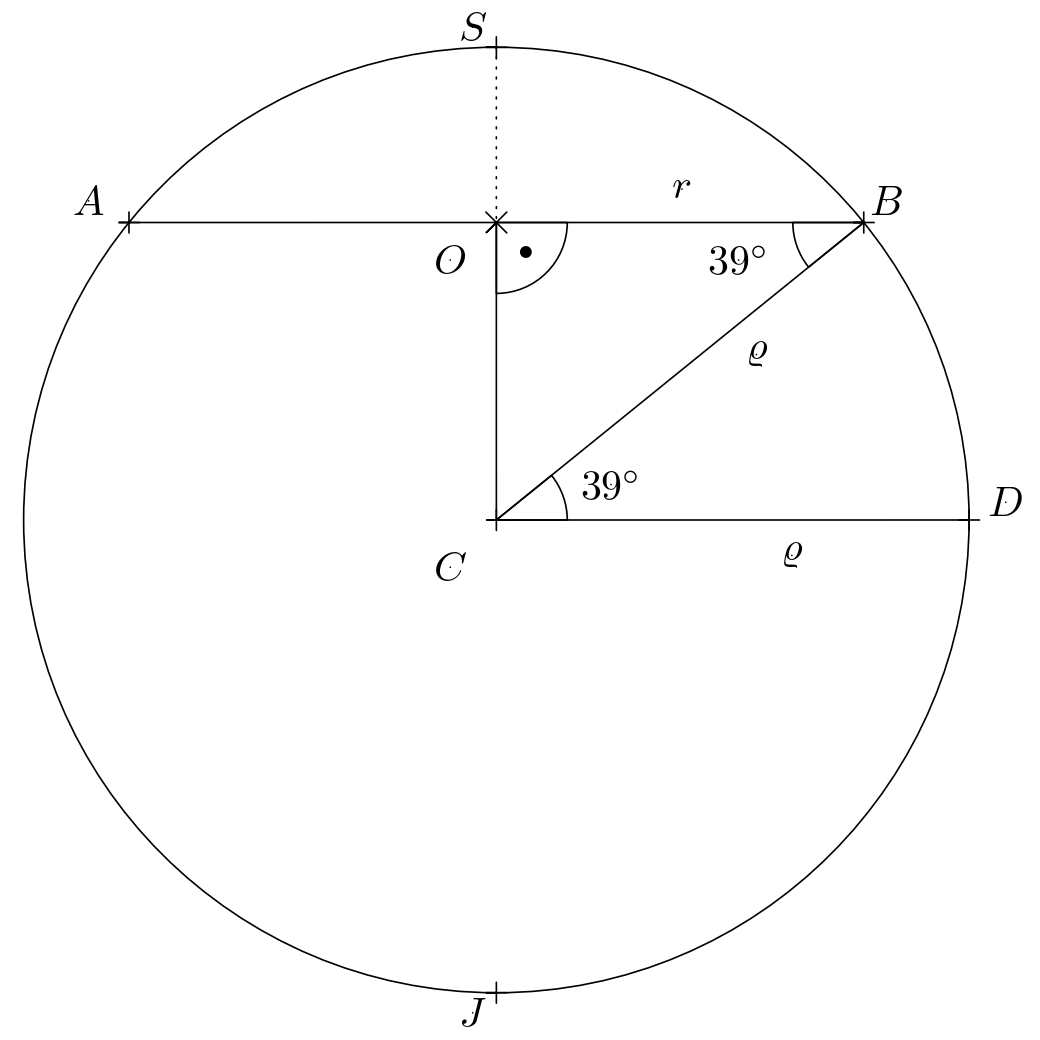
The figure shows the equality
$\lvert\sphericalangle CBO\rvert = \lvert\sphericalangle BCD\rvert$
(the angles are alternating) and by using the cosine function
-in the rectangular triangle $BSO$ we get $r=\varrho\cdot \cos 39^{\circ}$.
+in the right-angled triangle $BSO$ we get $r=\varrho\cdot \cos 39^{\circ}$.
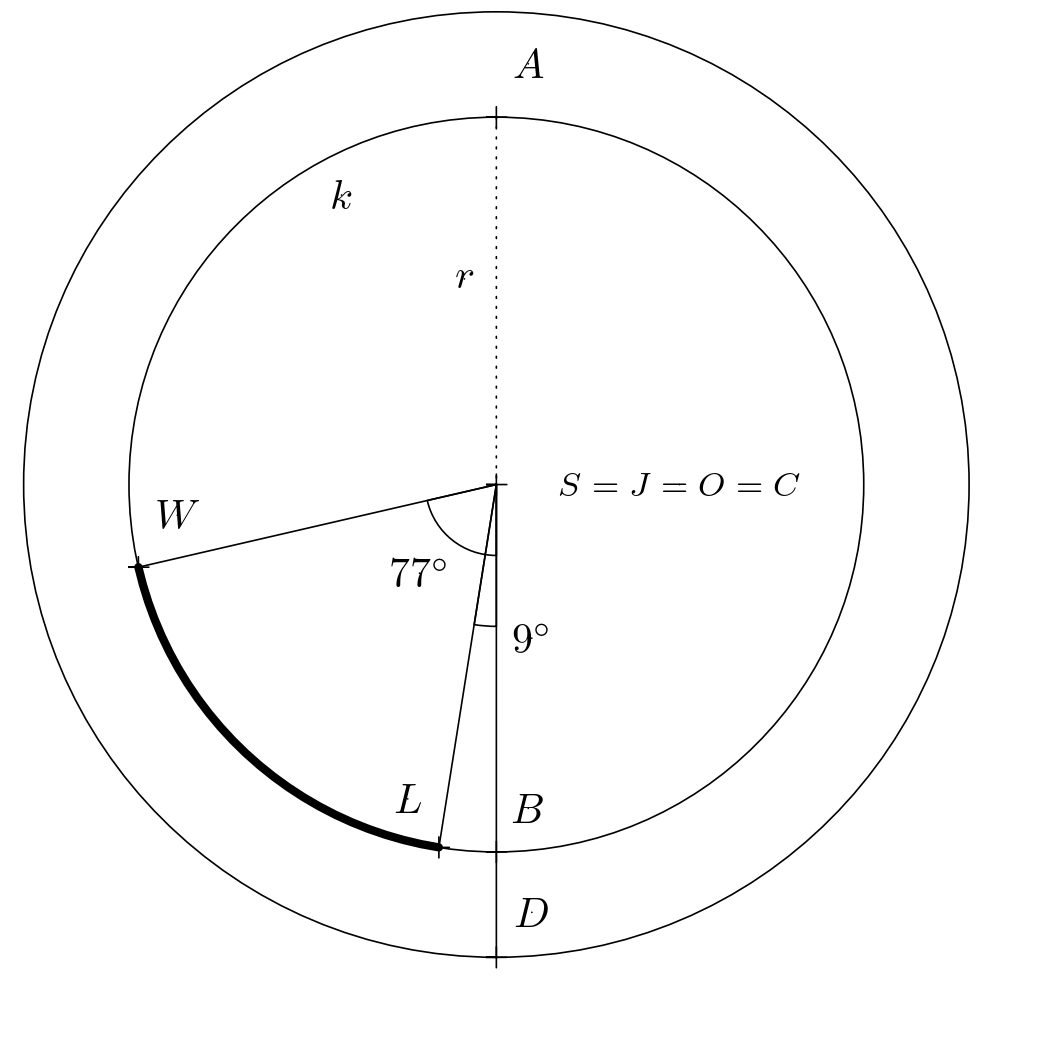
-The trajectory of a plane moving along a parallel (in the figure below,
+The trajectory of the plane moving along the parallel (in the figure below,
the plane's trajectory is represented by the shorter arc $LW$)
-is determined by direct proportion: the whole circle $k$ has a length of
+is determined using direct proportion: the whole circle $k$ has a length of
$2\pi r =2\pi\varrho\cdot\cos 39^{\circ} \,\text{km}$,
i.e. the length of the shorter arc $LW$ is equal to
$$
-\frac{(77-9)}{360}\cdot 2\pi\varrho\cdot \cos 39^{\circ} \doteq 5\ 885{,}4\,\text{km}.
+\frac{(77-9)}{360}\cdot 2\pi\varrho\cdot \cos 39^{\circ} \doteq 5,885{.}4\,\text{km}.
$$
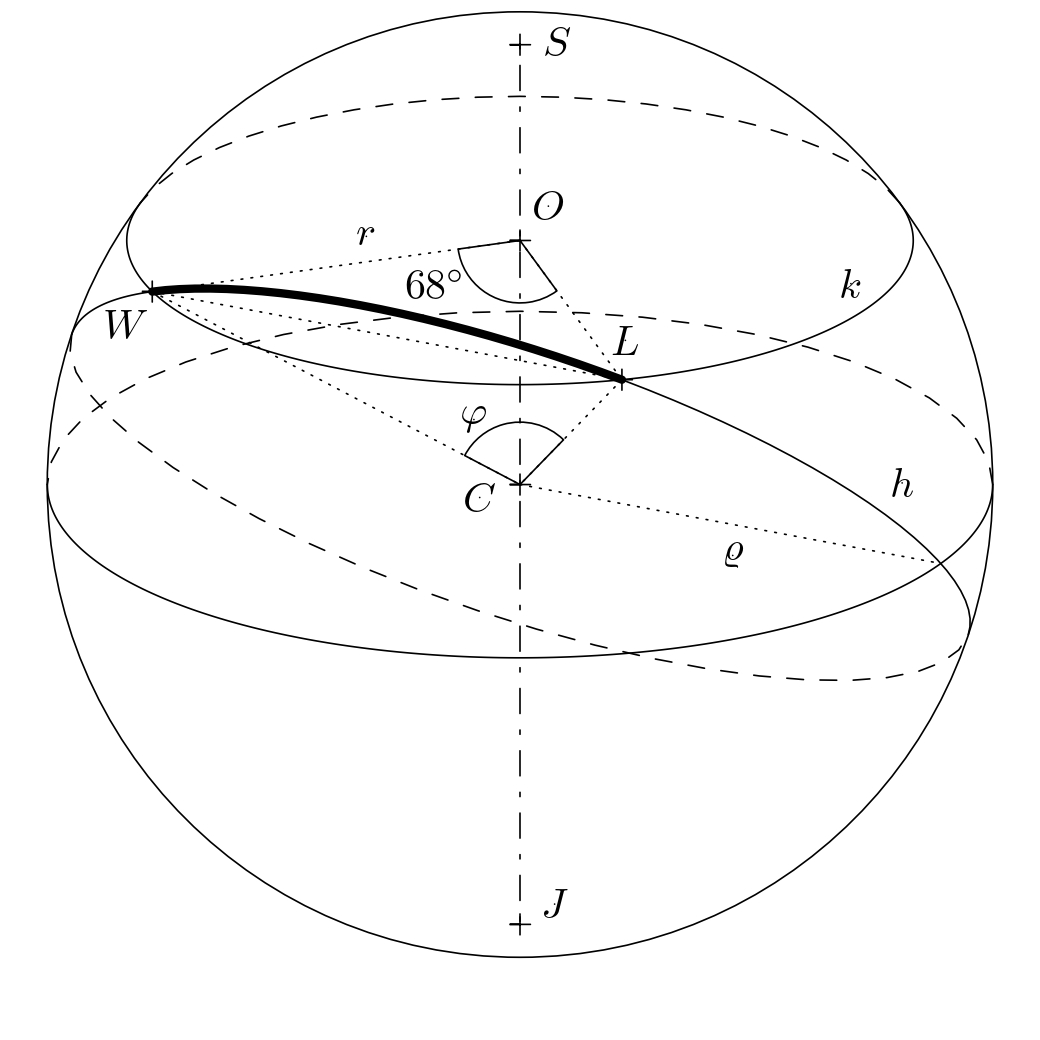
+Now, we determine how many kilometers the airplane covers while moving along the orthodrome.
+This is essentially the distance between two points on an imaginary sphere with the radius of $\varrho=6,381\,\text{km}$.
+The figure shows that the orthodrome between points $L$ and $W$ is an arc of a certain great circle $h$ with an
+unknown central angle $\varphi$. We need to determine the measure of this angle.
+
+
+
Let us consider an isosceles triangle $OWL$,
which we bisect with the height to the base $LW$ into two congruent right triangles.
-In either of these two triangles, then $\frac{|LW|}{2}=r\cdot \sin 34^{\circ}$ holds,
+In either of these two triangles, then the equation $\frac{|LW|}{2}=r\cdot \sin 34^{\circ}$ holds,
and thus $|LW|=2r\cdot\sin 34^{\circ}$.
-If we make a similar consideration for the isosceles triangle $CWL$,
+If we follow similar reasoning for the isosceles triangle $CWL$,
we get the equality $|LW|=2\varrho \cdot \sin\frac{\varphi}{2}$.
By comparing the right sides of both derived equalities,
we calculate the required angle $\varphi$:
@@ -93,13 +96,13 @@ $$
\frac{\varphi}{2}= \arcsin \left( \cos 39^{\circ}\sin 34^{\circ} \right) \doteq 25^{\circ}45' \quad \Rightarrow \quad \varphi \doteq 51^{\circ}30'.
$$
-We will determine the trajectory of the aircraft moving along the orthodrome similarly
-as in the case of a parallel line by direct proportion.
+We determine the trajectory of the airplane traveling along the orthodrome similarly
+as in the case of a parallel line using direct proportion.
The length of the whole circle $h$ is equal to $2\pi\varrho$.
-Then, for the length of the shorter arc $LW$, the following applies
+Then, for the length of the shorter arc $LW$, the following calculation applies
$$
-\frac{51{,}5}{360}\cdot 2\pi\varrho \doteq 5\ 735{,}5 \,\text{km}.
+\frac{51{.}5}{360}\cdot 2\pi\varrho \doteq 5,735{.}5 \,\text{km}.
$$
We see that the two trajectories differ by approximately $150 \,\text{km}$.