diff --git a/00005_Solid_Geometry-Cone_Cap/en_article_proofreading.md b/00005_Solid_Geometry-Cone_Cap/en_article_proofreading.md
index c14f8b9..929c95f 100644
--- a/00005_Solid_Geometry-Cone_Cap/en_article_proofreading.md
+++ b/00005_Solid_Geometry-Cone_Cap/en_article_proofreading.md
@@ -5,36 +5,43 @@ keywords:
is_finished: False
---
-# Conical cap
+# Carnival Hat
+<!--“cap” je kšiltovka, navíc název neodpovídal české verzi-->
-Eight-year-old Annie wants to go to a children's carnival in a white lady costume, which will include a white cone-shaped hat. The parents took the opportunity to practice their geometric imagination with Anna and decided to make the hat with her instead of buying it.
+Eight-year-old Annie wants to attend a children's carnival in a white lady costume, complete with a conical-shaped white hat. Her parents took the opportunity to involve Annie into honing her geometric imagination and decided to craft the hat with her instead of buying it.
+<!-- Úpravy v tomto odstavci jsou spíše kosmetické, ale myslím, že k lepšímu. Tj, neměním význam vět. Podobně i dále. Další komentáře jsou k důležitějším změnám.-->
-> **Exercise.** Anna and her mother found out with a tape measure that the circumference of Anna's head is 52 cm. Together they further agreed that the hat would be 30 cm high. How will they create the hat?
+**Exercise.** Annie and her mom used a tailor’s tape to measure and found out that the circumference of Annie's head is 52 cm. Then they agreed that the hat should be 30 cm tall. How will they create the hat?
+<!--tady se jméno Annie změnilo na Anna ?? Přijde mi lepší v příkladu zůstat konzistentně u jedné varianty jména. -->
-*Solution.* The cap is formed by the lateral surface/face of a cone, where we know the perimeter of the base $o$ (52 cm) and the height of the cone $v$ (30 cm). The unrolled lateral face of the cone is then a circular sector with an unknown radius $s$ (the size of the side of the cone) and an unknown central angle $\varphi$. We need to calculate these data. Furthermore, we know that the arc length of a circular sector is equal to the perimeter of $o$.
+*Solution.* The hat is formed from the lateral surface of a cone, where we know the base circumference $o$ (52 cm) and the cone height $v$ (30 cm). The unfolded lateral surface of the cone is then a circular sector with an unknown radius $s$ (the length of the cone’s side) and an unknown central angle $\varphi$. We need to calculate these values. Additionally, the length of the circular sector’s arc matches the base circumference $o$ of the cone.
+<!-- Pro obvod kruhu a délku je správný termín “circumference”. “perimeter” je obvod obdelníkové oblasti nebo oblasti ohraničené rovnými úseky. -->
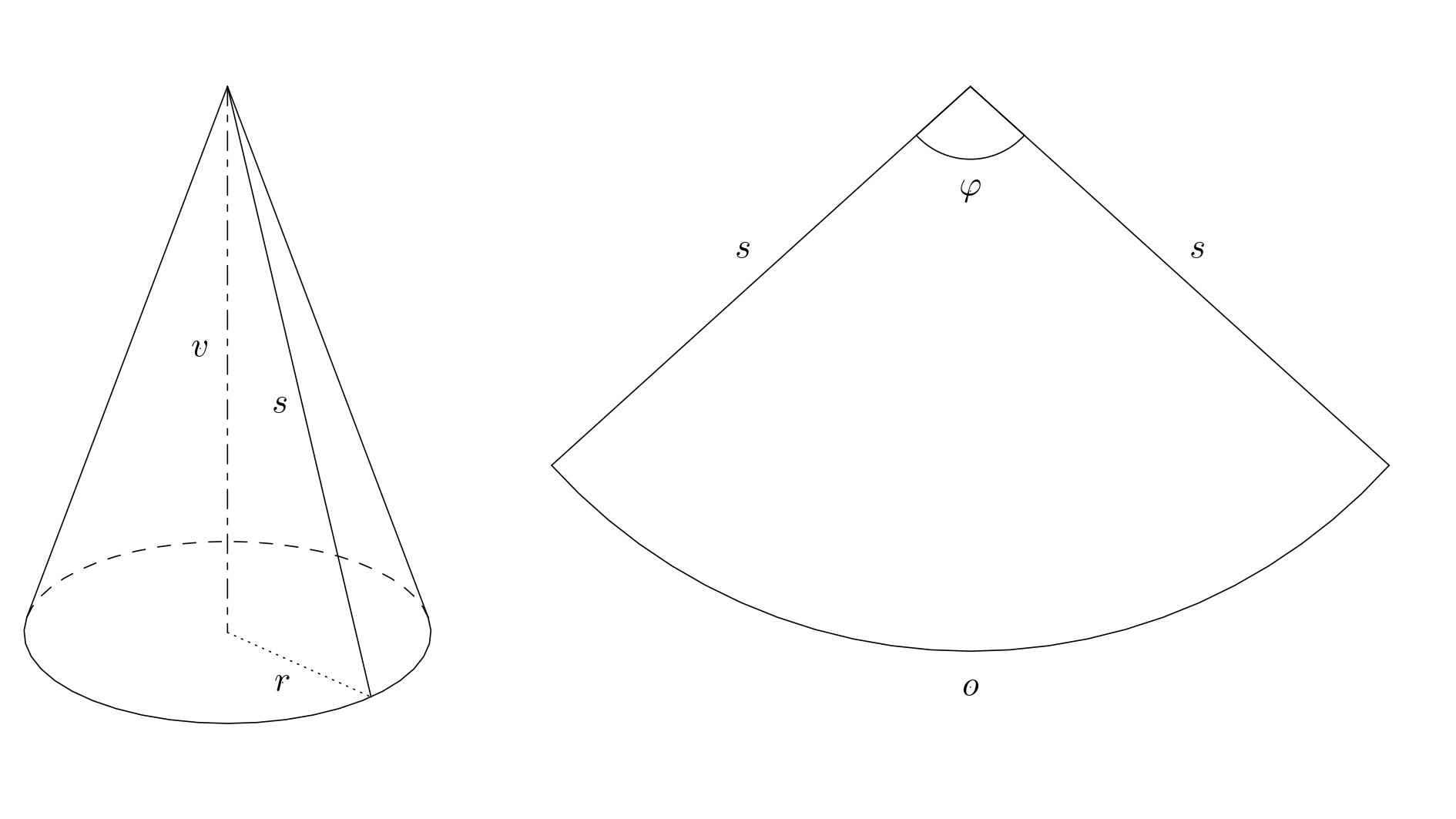
-First, we calculate the radius of the base $r$ from the perimeter of the base and then the length of the side $s$ using the Pythagorean theorem.
+First, we calculate the base radius $r$ from the known base circumference:
$$
r = \frac{o}{2\pi} = \frac{52}{2\pi} \doteq 8{,}28\,\text{cm}
$$
+Then, using the Pythagorean theorem, we find the side length $s$:
+
$$
s = \sqrt{v^2 + r^2} = \sqrt{30^2 + 8{,}28^2} \doteq 31{,}12\,\text{cm}
$$
-Now we determine the angle $\varphi$. First we calculate the perimeter $O$ of the whole circle of radius $s$, we get
+Now, we determine the angle $\varphi$. First, we calculate the perimeter $O$ of the whole circle of radius $s$:
$$
O = 2\pi s \doteq 195{,}53 \,\text{cm}.
$$
-Next, we use the direct proportionality between the arc length of this circle and the corresponding central angle to calculate the angle $\varphi$:
+Next, we use the direct proportionality between an arc length and the corresponding central angle of a circular sector for the given circle to calculate the measure of the angle $\varphi$:
+<!--“of this circle” je správně přeloženo z češtiny, ale nedává mi to správný smysl. Tj. přímá úměrnost mezi délkou oblouku a velikostí vnitřního úhlu platí obecně pro daný poloměr. Formulaci jsem upravila tak, aby přesněji vystihovala popisovaný vztah. (Formulace není moc šikovná ani v češtině - možná by to taky stálo za zpřesnění.)-->
$$
\varphi = \frac{o}{O}\cdot 360^{\circ} = \frac{52}{195{,}53}\cdot 360^{\circ} \doteq 95^{\circ}44'.
$$
-Annie and her parents create a hat out of a circular sector with an approximate radius of 31 cm and a central angle of approximately $96^{\circ}$.
+Annie and her parents will create the hat from a circular sector with an approximate radius of 31 cm and the central angle of approximately $96^{\circ}$.