diff --git a/00002_pyramid_game/en_article_proofreading.md b/00002_pyramid_game/en_article_proofreading.md
index e313e44..651267a 100644
--- a/00002_pyramid_game/en_article_proofreading.md
+++ b/00002_pyramid_game/en_article_proofreading.md
@@ -4,53 +4,45 @@ author: Math4U, Jakub Novák
---
# Geometric sequence - pyramid scheme
+Imagine someone, on behalf of an investment company, offers you a quick way to grow your money.
+The only thing you need to do is to convince three of your friends to invest as well.
+However, your money won't actually be used to buy gold or stocks, it will be split between the people who joined the company before you.
+If you can convince three friends to join, you'll get a share of their money and also a portion from the other people they convince.
+This continues until the whole model collapses for lack of new investors and the company’s owner mysteriously flies off to the Bahamas.
+It has to be said that this sort of thing is not good for friendships.
-Imagine someone offers you
-a quick appreciation of your money on behalf of an investment company. All you have to do is
-to convince three other friends to invest. However, your money
-won't be used actually to buy gold or stocks, it will be split
-between the people who signed up for the company before you. If you
-can convince three friends, you'll get a share of their money and
-also from the other people they convince - until the whole model
-collapses for lack of new investors and the owner of the company mysteriously
-flies off to the Bahamas. It has to be said this sort of thing
-is not good for friendships.
-
-You've just fallen for one of the most widespread business scams scam
-models – *pyramid scheme*.
+You've just fallen victim to one of the most widespread fraudulent business models – *pyramid scheme*.
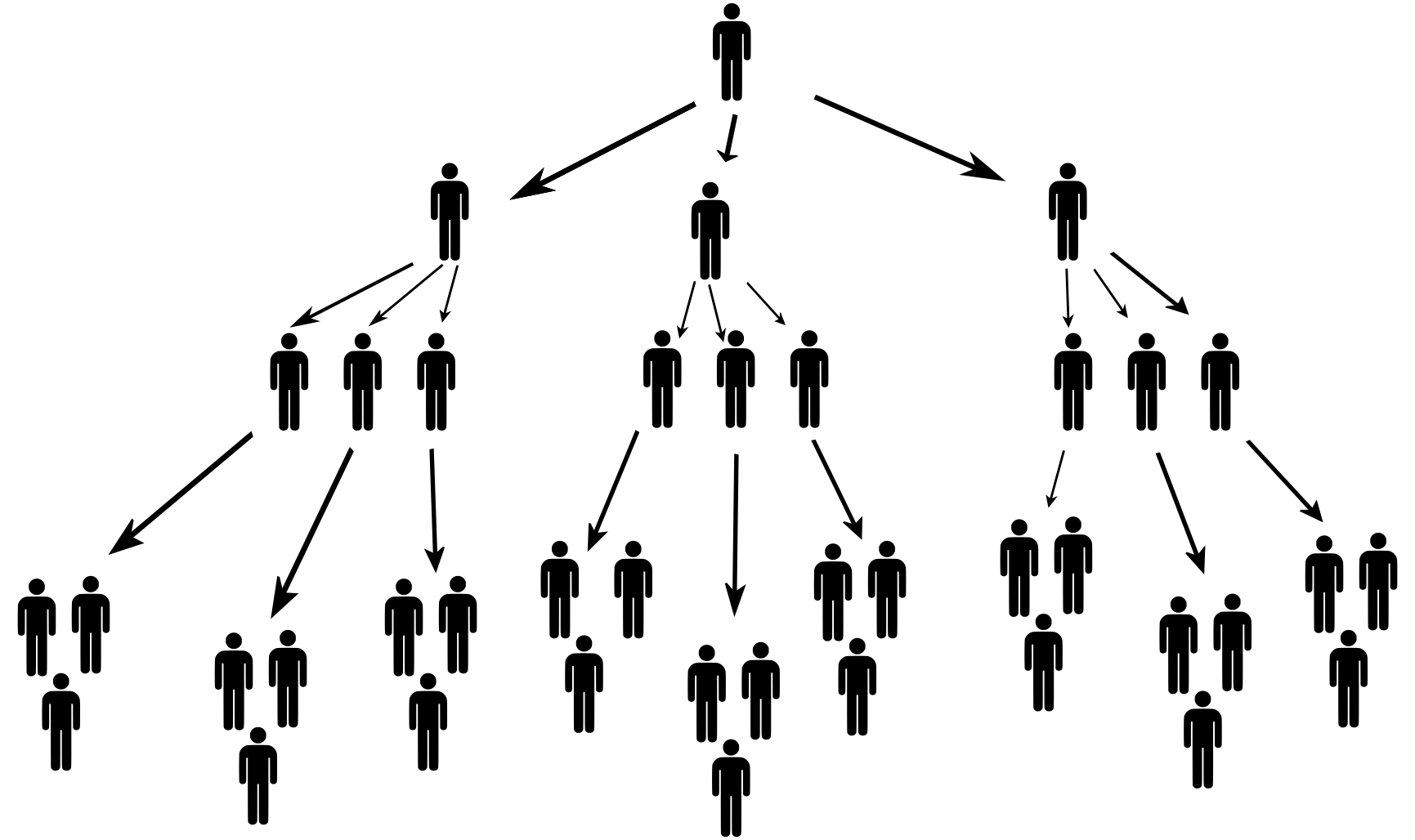
# Assignment
-The founder of the company (first level of the pyramid) gets three investors
-(second level of the pyramid) and collects a fixed entry fee from each
-20 000 CZK. The task of each of the three investors is to bring three new investors (third level of the pyramid)
-into the scheme and collect from each of them
-entry fee of 20 000 CZK. The same is repeated for the other levels. For
-simplicity, we will assume that the recruitment of new members always occurs
-only after the entire pyramid level is filled - i.e. recruiting new members to
-the fourth level begins after recruiting all nine investors in the third
-level.
-
-The entry fee of the new members is distributed among the existing
-new members as follows. 6 000 CZK will be given to person A who brought the new person,
-1 000 CZK will be given to person B who brought person A, the other
-1 000 CZK will go to person C who brought person B, another
-1 000 CZK will go to person D, who brought person C, and so on until there is no entry
-the entry fee is split. If the money is paid to the founder
-of the company, he gets the rest of the fee.
-
->**Exercise 1.** When will the newcomer get a refund on the joining fee?
-
-*Solution.* A newcomer pays an entry fee of 20 000 CZK. In order to get the money back, he must recruit three new members (from whom he will receive a total of 18 000 CZK) and they must recruit at least two more members (from whom he will receive the remaining 2 000 CZK).
+
+The founder of the company (the first level of the pyramid) recruits three investors
+(the second level of the pyramid) and collects a fixed entry fee of 20 000 CZK from each of them.
+The task of each of the three investors is to bring in three new investors into the scheme
+(the third level of the pyramid) and collect an entry fee of 20 000 CZK from each of them.
+The same process is repeated for the subsequent levels. For simplicity, we will assume that the recruitment
+of new members always occurs only after the entire pyramid level is filled. For example, recruiting new members
+into the fourth level only begins after recruiting all nine investors to the third level.
+
+The entry fee paid by new members is distributed among existing participants as follows:
+6 000 CZK will be given to person A, who brought in the new person,
+1 000 CZK will be given to person B, who brought in person A, another
+1 000 CZK will go to person C, who brought in person B, another
+1 000 CZK will go to person D, who brought person C, and so on until the entry fee is divided.
+If the money is paid to the founder of the company, he gets the rest of the fee.
+
+>**Exercise 1.** When will the newcomer get a refund for the joining fee?
+
+*Solution.* A newcomer pays an entry fee of 20 000 CZK. In order to get the money back, they must recruit three new members, from whom they will receive a total of 18 000 CZK. Additionally, these recruited members must each bring in at least two more members, from whom the newcomer will receive the remaining 2 000 CZK.
>**Exercise 2.**
>When a certain level of the pyramid is reached, the founder of
>the company does not receive money from the entry fees for the first time.
>
>1. Which level is it?
->2. How many people are in the whole pyramid after this level is reached? Compare this number with the number of people in your school or community.
->3. Determine the percentage of people who are in loss after this
+>2. After reaching this level, how many people are there in the entire pyramid? Compare this number to the number of people in your school or community.
+>3. Determine the percentage of people who are in a loss after this
> level is reached.
*Solutions of Exercise 2.*
@@ -66,8 +58,9 @@ and the seventeenth term of the geometric sequence: $a_{16}+a_{17}=3^{15}+3^{16}
$$P=100\cdot\frac{57\ 395\ 628}{64\ 570\ 081}\doteq 88{,}89\ \%.$$
>**Exercise 3.**
->In real cases from the Czech Republic, the number of participants was in the order of units of thousands. Let's say, therefore, that the number of participants in our
-pyramid after a certain level has been reached is between 2 000 and 8 000.
+>In real cases from the Czech Republic, the number of participants was in the order of units of thousands.
+>Therefore, let's say that the number of participants in our
+pyramid is between 2 000 and 8 000, after reaching a certain level.
>1. Which level is it?
>2. Determine the percentage of people who are now at a loss.
>3. Determine the total profit of the founder of the company.
@@ -88,10 +81,9 @@ is 3 280 now).
We can notice that the result is not very different from the result in 2.3, even though the
numbers of people considered are different in orders of magnitude.
-*Solution of 3.3.* The founder of the company receives the entire input from each person in the second level
+*Solution of 3.3.* The founder of the company receives the entire input fee from each person in the second level
fee (20 000 CZK), from each person in the third level 14 000 CZK, from each person
-in the fourth level 13 000 CZK, etc. Since the pyramid has eight levels now, the total profit $Z_1$ of the founder is
-of the founders as
+in the fourth level 13 000 CZK, etc. Since the pyramid now has eight levels, the total profit $Z_1$ of the founder is
$$Z_1=3\cdot 20\ 000 + 3^2\cdot 14\ 000 + 3^3\cdot 13\ 000 + \cdots + 3^7\cdot 9\ 000 = 31\ 155\ 000.$$
@@ -101,14 +93,14 @@ $$Z_1=3\cdot 20\ 000 + 3^2\cdot 14\ 000 + 3^3\cdot 13\ 000 + \cdots + 3^7\cdot 9
The red-colored investor in the second level of the pyramid receives 6 000 CZK from each of the three blue-colored investors in the third level. These three investors then recruited other people into the scheme. The red investor collects 1 000 CZK from each green colored investor. Similarly, he collects 1 000 CZK from people recruited by green investors and all other people in "his" branch of the pyramid.
-Let us now determine the profit of the red investor. The number of people from whom he receives 1 000 CZK is equal to the sum of $$3^2 + 3^3 + 3^4 + 3^5 + 3^6$$ (the whole pyramid should have eight levels). We must also not forget to deduct the entry fee. Thus $$Z_2=3\cdot 6\ 000 + (3^2+3^3 + 3^4 + 3^5 + 3^6 )\cdot 1\ 000 - 20\ 000 = 1\ 087\ 000.$$
+Let us now calculate the profit of the red investor. The number of people from whom he receives 1 000 CZK is equal to the sum of $$3^2 + 3^3 + 3^4 + 3^5 + 3^6$$ (the whole pyramid should have eight levels). We must also not forget to subtract the entry fee. Thus $$Z_2=3\cdot 6\ 000 + (3^2+3^3 + 3^4 + 3^5 + 3^6 )\cdot 1\ 000 - 20\ 000 = 1\ 087\ 000.$$
-*Solution of 3.5.* From Exercise 3.1, we know that there are a total of 3 280 people in the pyramid, each except for the founder paid 20 000 CZK in entrance fees. The total amount of money collected is therefore 65 580 000 CZK. From parts 3.3 and 3.4 we know the profit of the founder and the investor in the second level, so we will also calculate the profit of the investor in the third level (similarly to part 3.4): $$Z_3=3\cdot 6\ 000 + (3^2+3^3 + 3^4 + 3^5 )\cdot 1\ 000 - 20\ 000 = 358\ 000. $$ Now we can determine the share of funds paid out to people at the first three levels ($S$ is the total amount): $$P''=100\cdot\frac{Z_1 + 3\cdot Z_2 + 9\cdot Z_3}{S}=100\cdot\frac{37\ 638\ 000}{65\ 580\ 000}\doteq 57{,}39\ \%.$$ For a better understanding, it is important to realize that this share of the total "company income" is paid to only 13 people out of 3,280. Approximately $0{,}4\ \%$ of the people in the pyramid will thus receive more than half of the collected money. It is therefore not surprising that pyramid schemes are prohibited as a business model in a number of countries around the world (unfortunately, the Czech Republic is not among them until today, until 2023).
+*Solution of 3.5.* From Exercise 3.1, we know that there are a total of 3 280 people in the pyramid, each except for the founder paid 20 000 CZK in entrance fees. The total amount of money collected is therefore 65 580 000 CZK. From parts 3.3 and 3.4 we know the profit of the founder and the investor in the second level, so we will also calculate the profit of the investor in the third level (similarly to part 3.4): $$Z_3=3\cdot 6\ 000 + (3^2+3^3 + 3^4 + 3^5 )\cdot 1\ 000 - 20\ 000 = 358\ 000. $$ Now we can determine the share of funds paid out to people at the first three levels ($S$ is the total amount): $$P''=100\cdot\frac{Z_1 + 3\cdot Z_2 + 9\cdot Z_3}{S}=100\cdot\frac{37\ 638\ 000}{65\ 580\ 000}\doteq 57{,}39\ \%.$$ For a better understanding, it is important to realize that this share of the total "company income" is paid to only 13 people out of 3,280. Approximately $0{,}4\ \%$ of the people in the pyramid will thus receive more than half of the collected money. It is not surprising, therefore, that pyramid schemes are prohibited as a business model in a number of countries around the world (Unfortunately, the Czech Republic is not among them as of 2023.).
## Literature
-Yates K. *The Math of Life and Death: 7 Mathematical Principles That Shape Our Lives*. Scribner; Standard Edition (January 7, 2020).
+* Yates K. *The Math of Life and Death: 7 Mathematical Principles That Shape Our Lives*. Scribner; Standard Edition (January 7, 2020).
-Illinois Attorney General. *Pyramid schemes* [online]. Dostupné z
+* Illinois Attorney General. *Pyramid schemes* [online]. Dostupné z
<https://ag.state.il.us/consumers/pyramid.html> [cit. 1.6.2023].