diff --git a/00001_sea_navigation/en_article_proofreading.md b/00001_sea_navigation/en_article_proofreading.md
index 6b22c11..5d6b9f0 100644
--- a/00001_sea_navigation/en_article_proofreading.md
+++ b/00001_sea_navigation/en_article_proofreading.md
@@ -6,13 +6,15 @@ author: math4u project designed by Jakub Novák
# Circumference angles - ship navigation
Since the 15th century, navigators have been equipped with mechanical aids,
-that allowed them to measure the angular distance between two objects (e.g.
-stars, the Sun and the horizon, or significant points on distant land).
-Among such aids we mention here the Jacob's staff, the astrolabe or the marine sextant.[^1] It is interesting to note that despite its age, the
-the sextant in particular still has its place as a backup in the event of a sudden loss of GPS signal
+that allowed them to measure the angular distance between two objects (such as
+stars, the Sun, and the horizon, or significant points on a distant land).
+Among such aids, we mention here the Jacob's staff, the astrolabe, or the marine sextant.[^1] It is interesting to note that despite its age,
+the sextant, in particular, still has its place as a backup in case of a sudden loss of GPS signal
and is even being tested for its potential emergency use in space.
-[^2] Among other mechanical navigation tools, let us mention e.g.
-station pointer, whose role will be explained in the note after the solution of the first exercise.
+[^2] Among other mechanical navigation tools, let us mention the station pointer, whose role will be explained in the note after the solution of the first exercise.
+<!-- V odstavci jsem doplnila více čárek a provedla další úpravy:
+"e.g." jsem změnila na "such as" pro lepší čtivost (tj. není to nutná změna)
+"in the event" je myslím nešikovné, více se sem hodí/používá "in case" -->

@@ -20,57 +22,74 @@ station pointer, whose role will be explained in the note after the solution of
## Exercises
-In the following two exercises, there is a map for students to draw on. We provide the assignments also in the form of a printable worksheets.
-
+The following two exercises involve a map that students will need to draw on. Therefore, we provide the assignments also in the form of a printable worksheets.
+<!-- Po úpravě myslím text lépe vystihuje význam sdělení i ve srovnání s českou verzí.-->
[or: For each of following two exercises we provide a printable worksheets
with map for students to draw on.]: #
-> **Exercise 1.** The map shows the positions of three lighthouses near the town of Bonifacio on
-> Corsica. The captain of a ship at sea has measured two
-> angular distances $\theta$ of the pair of lighthouses as follows:
+> **Exercise 1.** On the map, the positions of three lighthouses near the town of Bonifacio on Corsica are marked.
+The captain of a ship at sea has measured two
+> angular distances, denoted $\theta$, between two pairs of lighthouses as follows:
>
> * $\theta (2,3) = 52°$
> * $\theta (1,3) = 35°$
>
> Construct a point on the map indicating the position of the ship at the time of measurement.
-> Assume that the measurements were taken in rapid succession, i.e. the ship's position
-> virtually unchanged.
-
+> Assume that the measurements were taken in rapid succession,
+ i.e., the ship's position practically did not change.
+<!-- V zadání jsem provedla více úprav. Dále je komentář jen k jedné:
+"between two pairs" odpovídá významu zadání oproti "of the pair", protože se měří úhlová vzdálenost mezi dvěma dvojcemi majáků-->
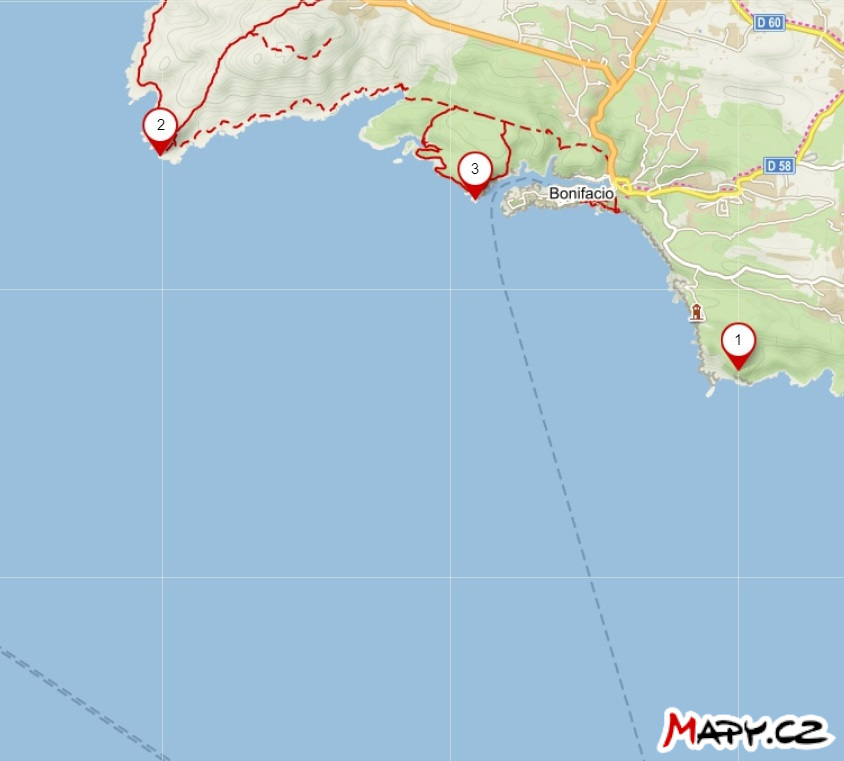
-*Solution.* If the angular distance between beacons $2$ and $3$ is $52°$, the ship is
-somewhere on the isoptics of a line segment (i.e. the set of points in the plane from which a given line segment can be seen at a given angle) with endpoints $2$ and $3$ corresponding to said
-angle. Similarly, it is also on the isoptics of a line segment equiangular of the line segment with endpoints $1$ and
-$3$ corresponding to the angle $35°$, so the ship must be at the intersection of the two circular arcs. Of course, we only consider those circular arcs that make sense.
-
+*Solution.* If the angular distance between lighthouses 2 and 3 is 52°, the ship is located somewhere on the circle that corresponds to a locus of a vertex of the angle 52° subtending a line segment with endpoints 2 and 3.
+Similarly, it is also located on the circle that is a locus of a vertex of the angle 35° subtending a line segment with endpoints 1 and 3.
+So, the ship must be at the intersection of these two circles. Of course, we only consider those circular arcs that make sense.
+<!-- Tento odstavec jsem hodně měnila. Hlavně proto, že si myslím, že "isoptic" není správný termín pro "ekvigonálu". Bohužel, ekvivalent ekvigonály si myslím se v angličtině nepoužívá.
+Zde je odkaz na příklad textu, kdy jde o úlohu nalezení ekvigonály v angličtině: http://jwilson.coe.uga.edu/emt725/AngleSubtendSegment/AngleSubtendSeg.html
+Zde je příklad definice "isoptic curve", což ekvigonále neodpovídá:
+https://mathworld.wolfram.com/IsopticCurve.html
+Neměli bychom od středoškoláků očekávat, že buou rozumět správně co se myslí pojmem "isoptic"ani jinou náhradou pro ekvgonálu, když se to v angličtině nepoužívá.
+-->
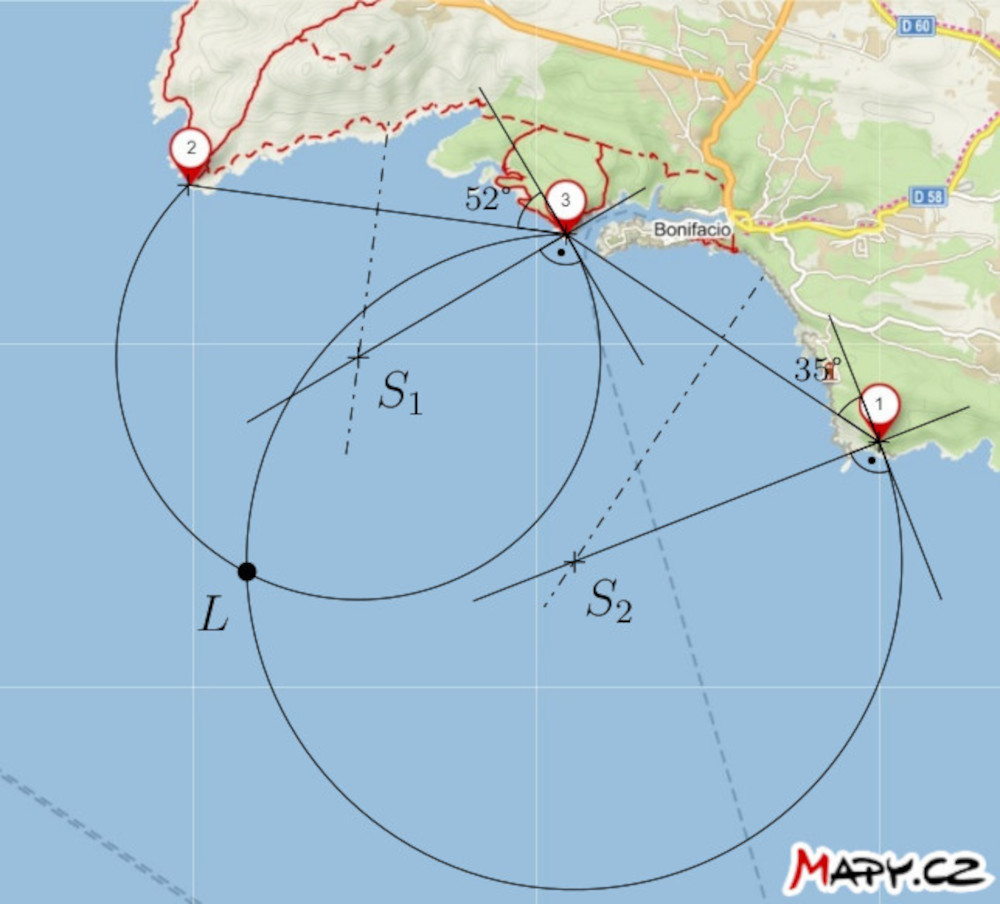
-**Note.** The tool that freed navigators from this construction is the three-armed protractor (station pointer) we already mentioned. Its three arms were set on the map in such a way that they pass through positions of the three salient points and form angles of the measured sizes. The intersection of the arms then determined the position of the ship on the map.
-
-> **Exercise 2.** On the map of the strait between the islands of Mallorca and Menorca, two significant
-> points on the mainland and the position of the ship $L$ are marked. In addition, there are indicated
-> two areas of dangerous waters in which there are underwater obstacles.
-Find a way to sail the boat through the dangerous waters to Cala
-> Agulla harbour. Take advantage of the ship captain's ability to measure
-the angular distance between the two points in question.
-
+**Note.** The tool that freed navigators from this construction is the station pointer (also called the three-armed protractor) we already mentioned. Its three arms were set on the map in such a way that they passed through positions of the three salient points and formed angles of the measured sizes. The intersection of the arms then determined the position of the ship on the map.
+<!-- Doporučuji prohodit názvy "station pointer" a "three-armed protractor", protože zmíněný výše je "station pointer"
+Dále jsem v odstavci upravila časy, aby text byl konzistentně v minulém čase.
+-->
+
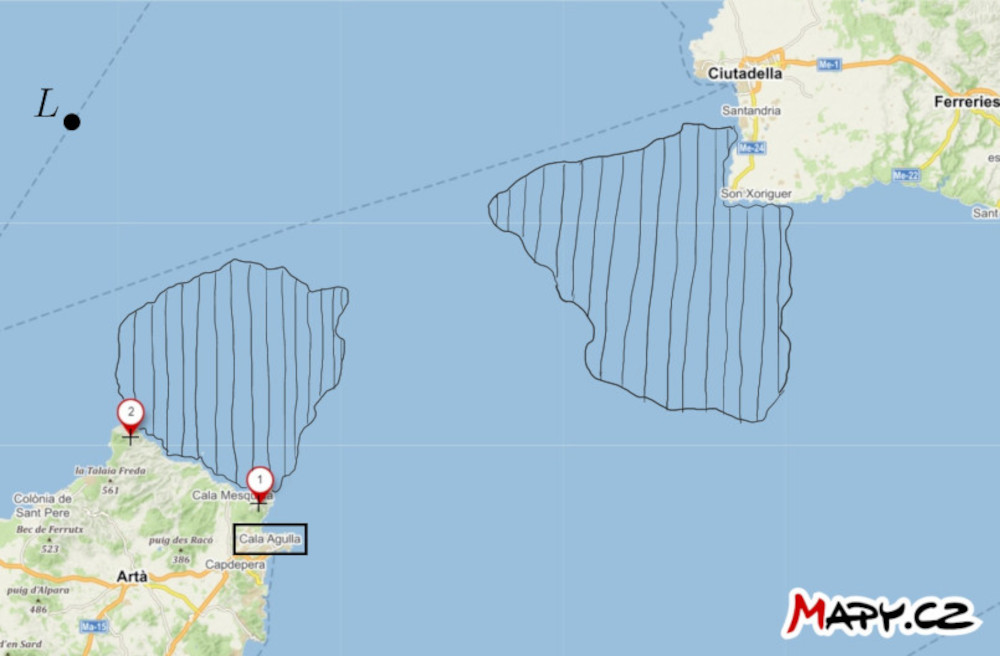
+> **Exercise 2.** On the map of the strait between the islands of Mallorca and Menorca, two prominent
+> points on the mainland and the position of the ship $L$ are marked. Additionally,
+> two areas of dangerous waters, containing underwater obstacles, are indicated.
+Find a way for the ship to navigate through the dangerous waters to the port of Cala Agulla.
+ Utilize the ship captain's ability to measure
+the angular distance between the two mentioned points at any given moment.
+<!-- Úpravy:
+"prominent" se mi líbí více než "significant", tj. to není nutná změna :-)
+Další úpravy "doufám" zlepšují čtivost a usnadňují porozumění textu.Za důležíté vzhledem k významu zadání považuji zmínku, že kapitám může měřit čas "at any given moment", podobně jak je to v české verzi.-->
-*Solution*. Construct the major arcs of the circles $k_1$ and
-$k_2$ that pass through points $1$ and $2$ (centers of the arcs are on the axis of the line segment with endpoints $1$ and $2$) and which have the following additional property:
-the arc of the circle $k_1$ tightly encloses the dangerous area closer to the port and the arc of the circle $k_2$ is tangent to
+*Solution*. Let us construct the larger arcs of the circles, denoted $k_1$ and
+$k_2$ passing through points $1$ and $2$. The centers of the circles are on the axis of the line segment with endpoints $1$ and $2$. The circles have the following additional property:
+the arc of circle $k_1$ tightly encloses the dangerous area closer to the port, and the arc of circle $k_2$ is tangent to
the more distant area. Each of these arcs is a subset of some
-isoptics of a line segment $12$. Let us now measure an inscribed angles corresponding to these arcs. It is approximately $33°$ for the arc of the circle $k_1$ and $20°$ for the arc of circle $k_2$ in our situation.
+locus of a vertex of an angle subtending the line segment with endpoints $1$ and $2$. Now, let us measure the inscribed angles corresponding to these arcs. In our situation, the angle is approximately $33°$ for the arc of circle $k_1$ and $20°$ for the arc of circle $k_2$.
+<!-- Tento odstavec je více uraven.
+Upravovala jsem slovosled, členy. Odstranila "nadbytečnou" závorku.
+!!! Poznámku mám ke značení kružnic -k1 a k2. Myslím, že by toto značení mělo být použito v obrázku- což není.
+Text jsem dále přeformulovala tak, abych se vyhla termínu "isoptic"..-->
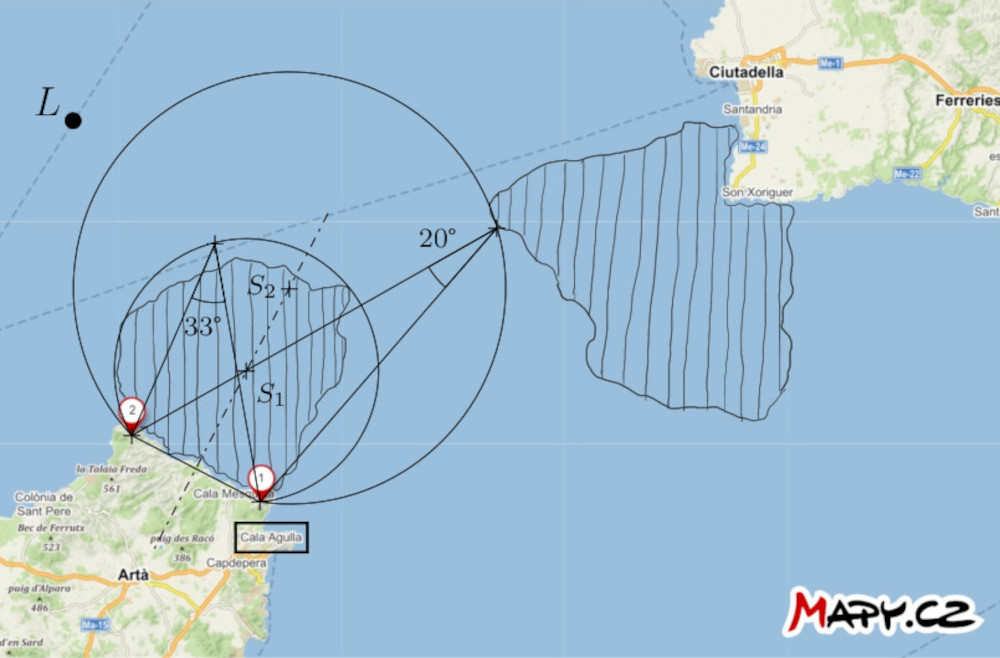
-If the arc distance of points $1$ and $2$ with respect to the ship is less than
+If the angular distance between points $1$ and $2$ with respect to the ship is less than
$33°$, we can say that the ship is confidently outside the danger zone
-closer to port. Conversely, if said arc distance is greater than
-than $20°$, the ship is outside the danger zone farther from the port.
-
-Let us now formulate a passage strategy: the captain of the ship will head in a straight direction for example to the point $2$ and during the voyage captain measures the arc distance of points $1$ and $2$. When
-this distance is greater than $20°$ (but still less than $33°$), the ship turns to the left in the direction of sailing and round the danger point by making an angular distance of the two points relative to the ship between $20°$ and $33°$. Thus ensure that the boat remains in a safe area between the two arcs.
+closer to the port. Conversely, if the angular distance exceeds $20°$, the ship is outside the danger zone farther from the port.
+<!-- Hlavní úprava v tomto odstavečku je z nesprávné "arc distance of the points" na "angular distance between the points".-->
+
+Now, let us formulate a strategy for navigation: The captain of the ship should head in a straight direction towards point $2$ and measure the angular distance between points $1$ and $2$ during the journey. When
+this distance becomes greater than $20°$ but still less than $33°$, the ship should turn left in the direction of sailing, to navigate around the danger zone, by maintaining the angular distance between the two points relative to the ship between $20°$ and $33°$. This approach ensures that the ship remains in the safe area between the two arcs.
+<!-- Opět více úprav:
+"passage" jsem změnila na "navigation" ve smyslu konzistence s úpravami/termíny v předchozím textu. Podobně "boat" jsem změnila na "ship" jak je používáno výše.
+Další úpravy v odstavci jsou myslím k lepší srozumitelnosti,čtivosti textu. Případné připomínky k úpravám ráda proberu osobně (Teams). -->
## References and literature